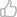圆周运动受力分析_匀速圆周运动受力分析
信息来源:互联网 发布时间:2025-03-15
圆周运动分为匀速圆周运动和变速圆周运动。首先确定物体做圆周运动的所在平面,然后垂直该平面上的合力为零,再找到指向圆心的力即为向心力。一:匀速圆周运动受力分析匀速圆周运动的合力即为向心力.例题:如图所示,摩天轮悬挂的座舱在竖直平面内做匀速圆周

圆周运动分为匀速圆周运动和变速圆周运动。首先确定物体做圆周运动的所在平面,然后垂直该平面上的合力为零,再找到指向圆心的力即为向心力。一:匀速圆周运动受力分析匀速圆周运动的合力即为向心力.


例题:如图所示,
摩天轮悬挂的座舱在竖直平面内做匀速圆周运动座舱的质量为m,运动半径为R,角速度大小为ω,重力加速度为g,则座舱()二:变速圆周运动受力分析物体所受的合力F不指向圆心,将F分解为跟圆弧相切的分力Ft和指向圆心的分力Fn.Fn产生向心加速度,方向与速度方向垂直,改变速度的方向;Ft产生切向加速度,切向加速度与物体的速度在一条直线上,改变速度的大小.。
三:一般曲线运动受力分析用圆周运动的分析方法处理一般的曲线运动,如图所示,
汽车在高低不平的路面上行驶时,不同位置上所对应的“圆周运动”的“圆心”和“半径”是不同的.例题:一般的曲线运动可以分成很多小段,每小段都可以看成圆周运动的一部分,即把整条曲线用一系列不同半径的小圆弧来代替.如图甲所示,
曲线上的A点的曲率圆定义为通过A点和曲线上紧邻A点两侧的两点作一圆,在极限情况下,这个圆就叫做A点的曲率圆,其半径ρ叫做A点的曲率半径.现将一物体沿与水平面成α角的方向以速度抛出如图乙所示则在其迹最高点P处的曲率半径是?
例题:如图所示,
长为L的轻杆,一端固定有一个质量为m的可视为质点的小球,另一端固定在水平转轴O上,杆随转轴O在竖直平面内匀速转动,角速度为ω,某时刻杆对球的作用力为F,方向恰好与杆垂直,此时杆与水平方向的夹角为θ.则下列关系正确的是(B )
例题:如图所示,
一圆盘可绕一通过圆心且垂直于盘面的竖直轴转动,在圆盘上放一块橡皮,橡皮随圆盘一起转动(俯视沿逆时针方向)某段时间内圆盘的转速不断增大,但橡皮仍相对圆盘静止在这段时间内,如图所示的橡皮所受合外力F 方向的四种表示(俯视图)中正确的是( )。
例题:一个小狗拉雪橇在水平面内圆弧轨道匀速行驶,如图所示画出了雪橇受到的牵引力F和摩擦力f之间的可能的方向关系示意图,其中正确的是:()
免责声明:本站所有信息均搜集自互联网,并不代表本站观点,本站不对其真实合法性负责。如有信息侵犯了您的权益,请告知,本站将立刻处理。联系QQ:1640731186